Perdite di carico in una condotta in pressione

Trattiamo il moto di fluidi incomprimibili in tubi cilindrici in pressione con portata costante.

Per il calcolo delle perdite di carico in una condotta è importante calcolare il numero di Reynolds per capire se si tratta di moto laminare (Re<1400) o turbolento (Re>2400). Tra 1400 e 2400 c'è una zona di transizione in cui "convivono" le caratteristiche del moto laminare e turbolento.
Il numero di Reynolds è dato da: 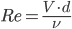, è la viscosità cinematica, 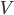la velocità media, d il diametro della condotta.

L'obiettivo è calcolare il numero di resistenza 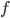per poter poi ricavare le perdite di carico secondo la formula iii) che verrà indicata più avanti.

Per entrambi i tipi di moto è possibile ricorrere al diagramma di Moody oppure a delle formule.

La cosa è piuttosto semplice per il moto laminare, dove il numero di resistenza (che è adimensionale) è dato da:

i)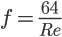  

Per il moto turbolento le cose si complicano un po', entra in gioco la "scabrezza" della condotta e si ricorre al già citato diagramma di Moody o alla formula di Colebrook-White (1939).

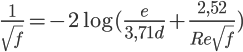
Si tratta di una formula non lineare e come tale un po' più ostica da trattare, potrete costruirvi un foglio excel che calcoli 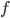con un po' di iterazioni. 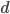è il diametro della condotta, Re il numero di Reynolds.
Vi riporto un po' di valori di (espressa in metri) per alcuni materiali (il mio riferimento bibliografico è: Augusto Ghetti "Idraulica")
Vetro, ottone, rame, piombo, tubi trafilati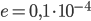
Tubi saldati senza sporgenze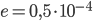
Ghisa asfaltata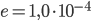
Ferro galvanizzato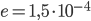
Ghisa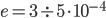
Calcestruzzo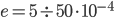
Tubi chiodati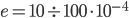

Nel caso di tubi lisci e fino a valori di Reynolds inferiori a 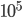si può utilizzare la formula di Blasius (1911). Normalmente queste condizioni sono realistiche per i circuiti oleodinamici, che operano in regime laminare o di transizione, quindi suggerisco di usare questa:

ii)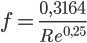  

Una volta ricavato il numero di resistenza 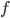, il calcolo delle perdite di carico è dato da:

iii)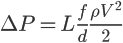  

Dove 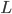è la lunghezza del tubo, 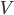la velocità media, la densità del fluido, 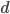il diametro medio, 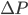la caduta di pressione espressa in Pascal. Ovviamente utilizzate sempre unità del S.I. (m, m/s, m³/s, kg/m³, Pa)

Un esempio pratico: consideriamo una tubazione da 1" (25,4 mm) lunga 2 m che porti 100 l/min di olio con viscosità di 46 cSt. La densità dell'olio è di 870 kg/m³.
La velocità è pari a 3,3 m/s, il numero di Reynolds 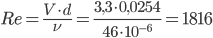 , siamo in regime di transizione.
Con la formula ii) ricaviamo il numero di resistenza: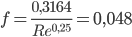
Dalla iii) 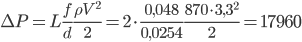 Pa, circa 0,2 bar